Introduction
A Radio Atmospheric signal or Sferic is a broadband electromagnetic impulse that generated by lightning discharges. The bulk of its energy concentrates within the ELF and VLF bands. For electromagnetic wave components in these frequency bands, both the D region of the ionosphere and ground are very good conductors. Consequently, the ionosphere and ground forms a waveguide and sferics may propagate from their lightning source without major attenuation in the waveguide for very long distances.
Introduction
A Radio Atmospheric signal or Sferic is a broadband electromagnetic impulse that generated by lightning discharges. The bulk of its energy concentrates within the ELF and VLF bands. For electromagnetic wave components in these frequency bands, both the D region of the ionosphere and ground are very good conductors. Consequently, the ionosphere and ground forms a waveguide and sferics may propagate from their lightning source without major attenuation in the waveguide for very long distances. They can be received even thousands of kilometers away from their source. This property has led to many applications, one of which is Global Lightning Geo-Location.
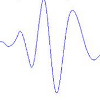
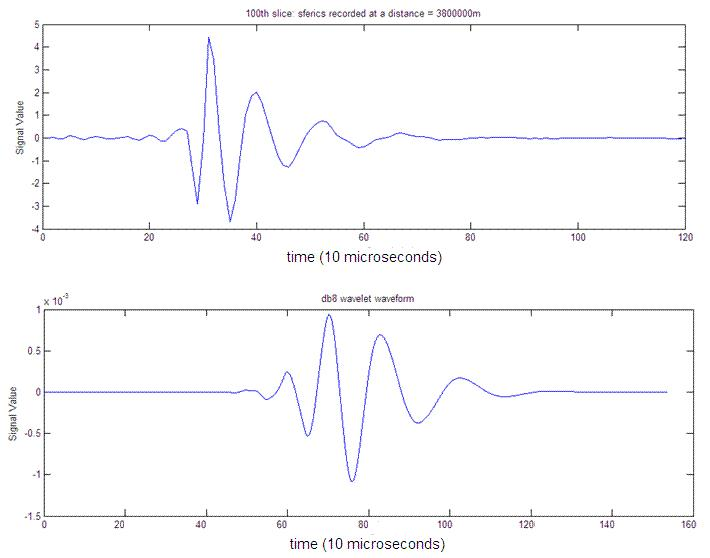
Current methods used in studying sferics are mostly in the time-domain and frequency-domain. Sferics appear to be relatively complicated signals in both domains. Due to the transient nature of sferics, wavelets may offer a different perspective that leads to sparse representations of sferics. In Figure 1, a specific sferic is compared to an atom function from a wavelet basis. The striking similarity between these two signals tends to suggest that in wavelet domain, sferics may have nearly singular representations.
Historically, sparse representations of signals associated with a physical system often lead to significant improvement in the understanding of the system. On the other hand, recent studies in the field of Compressive Sensing also shows some profound consequences of sparse signal representation for signal processing algorithms.
Research focus and current progress
This research starts with the basic observation shown in Figure 1 and move onto the study of the the sparsity of sferics representations in different wavelet domains as well as representations using redundant dictionaries.
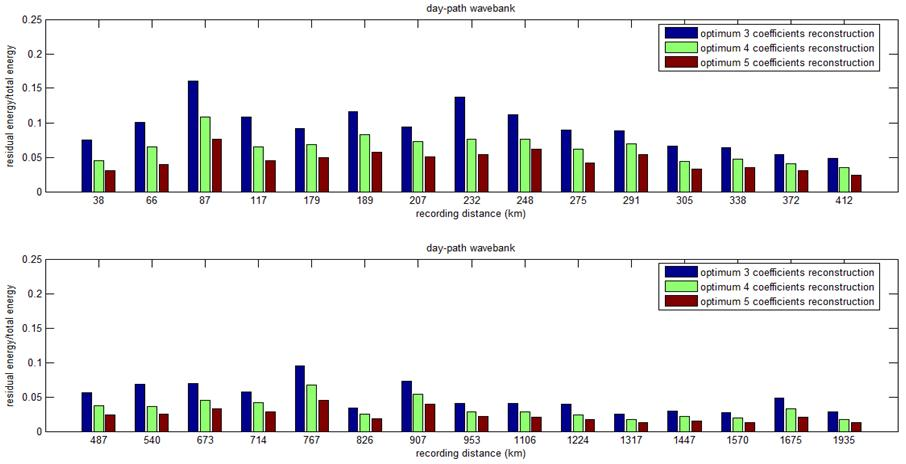
Figure 2 shows an example of the sparsity of wavelet representation of sferics obtained using OMP (orthogonal matching pursuit) method.
To produce this plot, all the sferics around the same location in a thunderstorm are averaged together to produce a low noise average waveform and then OMP method is applied to search for a optimal representation using a fixed number of coefficients. The vertical axis of the plots indicated the ratio between the error residual energy and the total energy of the original signal.
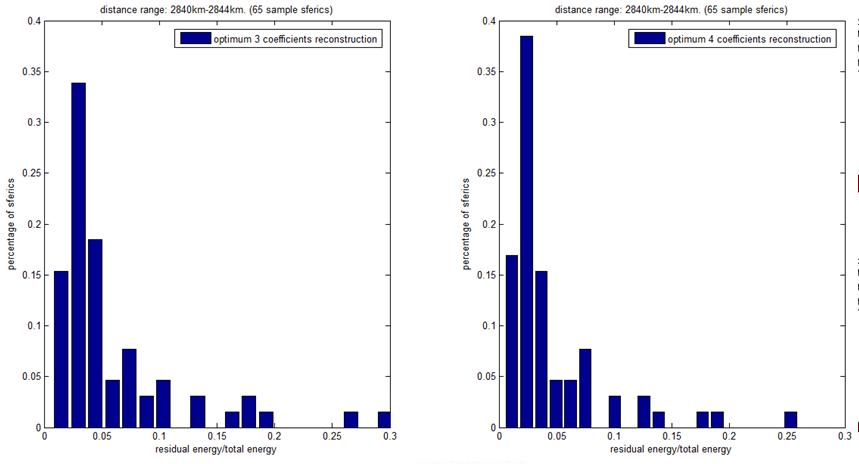
Figure 3 shows the histogram of the residual error of optimal representation with a fixed number of coefficients for a collection of individual sferics at similar distances from the lightning source.
Helpful references and links
K.G. Budden’s book “The Wave-Guide Mode THeory of Wave Propagation” provides an excellent explanation of the fundamental theories concerning EM wave propagation in the earth-ionosphere waveguide.
Information on some recent understanding and applications of sferics can be found at Global Lightning Geo-Location
Stephane Mallat’s book “A wavelet tour of signal processing” is a great tutorial for most signal processing methods involving wavelets.
http://dsp.rice.edu/cs
has a comprehensive collection of literatures on the topic of compressive sensing.