What is Chorus?
Whistler-mode chorus waves are one of the most common and most intense natural plasma waves occurring in the Earth’s outer magnetosphere (Helliwell, 1969; Allcock, 1957; Helliwell, 1965; Storey, 1953).
What is Chorus?
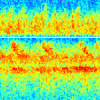
Whistler-mode chorus waves are one of the most common and most intense natural plasma waves occurring in the Earth’s outer magnetosphere (Helliwell, 1969; Allcock, 1957; Helliwell, 1965; Storey, 1953). Usually observed in the region outside of the plasmapause, chorus waves are discrete emissions often containing rising and falling tones, as well as short impulsive bursts (Burton and Holzer, 1974; Dunckel and Helliwell, 1969; LeDocq et al., 1998; Lauben et al., 2002; Sazhin and Hayakawa, 1992; Burtis and Helliwell, 1969). Chorus occurs over a broad frequency range, from hundreds of Hz up to about 10 kHz (Gurnett and O’Brien, 1964). Within this range, chorus waves typically occur in two distinct frequency bands, a lower band with frequencies 0.1
![]() 0.5
0.5![]() and an upper band with frequencies 0.5
and an upper band with frequencies 0.5
![]() 0.65
0.65![]() , where
, where ![]() denotes the equatorial gyrofrequency. There is typically a gap between these two bands at 0.5
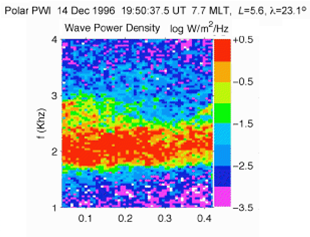
denotes the equatorial gyrofrequency. There is typically a gap between these two bands at 0.5![]() , where the wave power is at a minimum (Tsurutani and Smith, 1974; Burtis and Helliwell, 1976; Burtis and Helliwell, 1969). An example of this configuration, known as banded chorus, can be seen in Figure 1.
, where the wave power is at a minimum (Tsurutani and Smith, 1974; Burtis and Helliwell, 1976; Burtis and Helliwell, 1969). An example of this configuration, known as banded chorus, can be seen in Figure 1.
 |
Resonance Condition
Recent studies show chorus waves play a role in both the acceleration and precipitation of relativistic electrons through resonant scattering. This pitch angle scattering and energy diffusion can occur when the resonance condition,
![]() ,
, ![]() 0,
0, ![]() ,
, ![]() ,
, ![]() ,…, is satisfied. In this expression,
,…, is satisfied. In this expression, ![]() is the frequency of the wave,
is the frequency of the wave,
![]() and
and
![]() are the components of the wave vector and particle velocity parallel to the ambient magnetic field, respectively, m is the resonance harmonic number,
are the components of the wave vector and particle velocity parallel to the ambient magnetic field, respectively, m is the resonance harmonic number,
![]() is the local gyrofrequency, and
is the local gyrofrequency, and
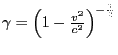 is the relativistic correction factor, where v is the particle velocity and c is the speed of light (Kennel and Petschek, 1966). The wave vector is typically specified with respect to the direction of the local magnetic field,
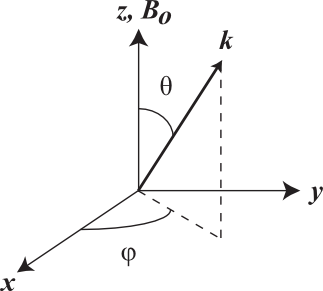
is the relativistic correction factor, where v is the particle velocity and c is the speed of light (Kennel and Petschek, 1966). The wave vector is typically specified with respect to the direction of the local magnetic field, ![]() , with the polar wave normal angle,
, with the polar wave normal angle, ![]() , defined as the angle between
, defined as the angle between ![]() and the wave vector (from 0
and the wave vector (from 0![]() to 180
to 180![]() ) and the azimuthal wave normal angle,
) and the azimuthal wave normal angle, ![]() , measured about the direction of
, measured about the direction of ![]() (from
(from ![]() 180
180![]() to 180
to 180![]() ). This coordinate system is illustrated in Figure 2, with the direction of
). This coordinate system is illustrated in Figure 2, with the direction of ![]() assumed to be in the z direction. The polar wave normal angle is needed to evaluate the resonance condition, while both
assumed to be in the z direction. The polar wave normal angle is needed to evaluate the resonance condition, while both ![]() and
and ![]() are needed to predict how the wave will propagate in the magnetosphere from its current location.
are needed to predict how the wave will propagate in the magnetosphere from its current location.
 |
Observations on the Polar Spacecraft
Wave normal analysis was done using observations of magnetospheric banded chorus on the Polar spacecraft. Launched on 2![]() 24
24![]() 1996, the Polar spacecraft has a highly elliptical, 86
1996, the Polar spacecraft has a highly elliptical, 86![]() inclination orbit with a period of approximately 17.5 hours, perigee of 1.8
inclination orbit with a period of approximately 17.5 hours, perigee of 1.8 ![]() , and apogee of 9
, and apogee of 9 ![]() . The Plasma Wave Instrument (PWI), onboard the Polar spacecraft, provides high-resolution plasma wave data within the chorus band. The PWI detects magnetic fields through the use of a triaxial magnetic search coil antenna (70
. The Plasma Wave Instrument (PWI), onboard the Polar spacecraft, provides high-resolution plasma wave data within the chorus band. The PWI detects magnetic fields through the use of a triaxial magnetic search coil antenna (70 ![]() V
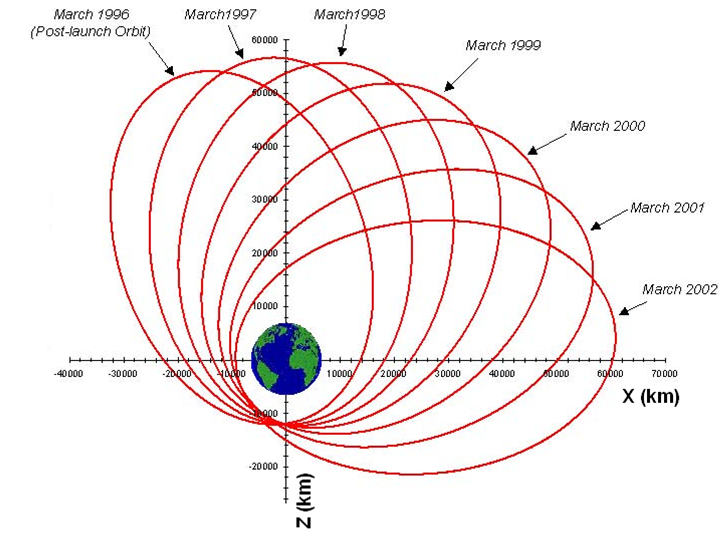
V![]() nT-Hz sensitivity) and detects electric fields using three orthogonal electric dipole antennas, two in the spacecraft spin plane (100 and 130 m, 6 s period), and one aligned along the spin axis (14 m). Images of the Polar spacecraft and its orbit are shown in Figures 3 and 4, respectively.
nT-Hz sensitivity) and detects electric fields using three orthogonal electric dipole antennas, two in the spacecraft spin plane (100 and 130 m, 6 s period), and one aligned along the spin axis (14 m). Images of the Polar spacecraft and its orbit are shown in Figures 3 and 4, respectively.
 |
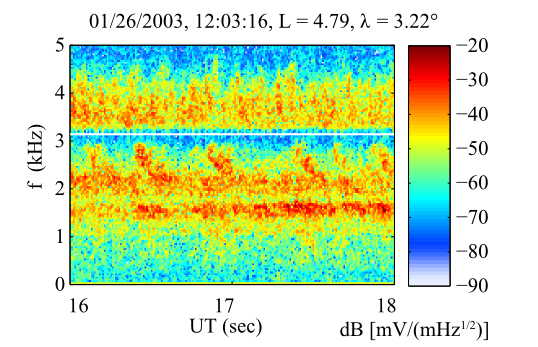
The signals from these antennas are processed by several receiver systems, one of which is the High Frequency Waveform Receiver (HFWR). Coincident sampling from 20 Hz to 25 kHz of 3 orthogonal components of the electric and magnetic wave fields is provided by the HFWR. In the high-telemetry rate mode, 0.45 second waveform snapshots are recorded from each antenna at intervals spaced 9.2 seconds apart (Gurnett et al., 1995). Figure 5 illustrates lower band chorus in one of these snapshots.
 |
Further Analysis of Banded Chorus
The results of the wave normal analysis using observations of banded chorus from the Polar spacecraft can be found in Haque et al. (2010). Using this data set from Polar, along with observations of chorus from other satellite systems, a theory of the source region of banded chorus is currently being tested. An overview of this theory is given in Bell et al. (2009).
Bibliography
Allcock, G. M. (1957), A study of the audio-frequency radio phenomenon known as
‘dawn chorus’, Aust. J. Phys., 10, 286-298.
Bell, T. F., U. S. Inan, N. Haque, and J. S. Pickett (2009), Source regions of
banded chorus, Geophys. Res. Lett., 36, L11101,
doi:
rm10.1029/2009GL037629.
Burtis, W. J., and R. A. Helliwell (1969), Banded chorus: A new type of VLF
radiation observed in the magnetosphere by OGO 1 and OGO 3, J.
Geophys. Res., 74, 3002-3010.
Burtis, W. J., and R. A. Helliwell (1976), Magnetospheric chorus: Occurrence
patterns and normalized frequency, J. Geophys. Res., 24,
1007-1024.
Burton, R. K., and R. E. Holzer (1974), The origin and propagation of chorus in
the outer magnetosphere, J. Geophys. Res., 79, 1014-1023.
Dunckel, N., and R. A. Helliwell (1969), Whistler-mode emissions on the OGO 1
satellite, J. Geophys. Res., 74(26), 6371-6385.
Gurnett, D. A., and B. J. O’Brien (1964), High-latitude geophysical studies
with satellite Injun 3, 5, Very low frequency electromagnetic radiation,
J. Geophys. Res., 69, 65-89.
Gurnett, D. A., A. M. Persoon, R. F. Randall, D. L. Odem, S. L. Remington,
T. F. Averkamp, M. M. DeBower, G. B. Hospodarsky, R. L. Huff, D. L. Kirchner,
M. A. Mitchell, B. T. Pham, J. R. Phillips, W. J. Schintler, P. Sheyko, and
D. R. Tomash (1995), The Polar plasma wave instrument, Space Sci.
Rev., 71, 597-622.
Haque, N., M. Spasojevic, O. Santolík, and U. S. Inan (2010),
Wave normal angles of magnetospheric chorus emissions observed on the Polar
spacecraft, Journal of Geophysical Research (Space Physics),
115, 0-+, doi:
rm10.1029/2009JA014717.
Helliwell, R. A. (1965), Whistlers and Related Ionospheric Phenomena,
Stanford Univ. Press, Stanford, Calif.
Helliwell, R. A. (1969), Low-frequency waves in the magnetosphere, Rev.
Geophys., 71(1, 2), 281-303.
Kennel, C. F., and H. E. Petschek (1966), Limit on stably trapped particle
fluxes, J. Geophys. Res., 71, 1-28.
Lauben, D. S., U. S. Inan, T. F. Bell, and D. A. Gurnett (2002), Source
characteristics of ELF/VLF chorus, J. Geophys. Res.,
107(A12), 1429, doi:
rm10.1029/2000JA003019.
LeDocq, M. J., D. A. Gurnett, and G. B. Hospodarsky (1998), Chorus source
locations from VLF Poynting flux measurements with the POLAR
spacecraft, Geophys. Res. Lett., 25, 4063-4066.
Sazhin, S. S., and M. Hayakawa (1992), Magnetospheric chorus emissions: A
review, Planet. Space Sci., 40, 681-697.
Storey, L. R. O. (1953), An investigation of whistling atmospherics,
Phil. Trans. R. Soc. London, A246, 113-141.
Tsurutani, B. E., and E. J. Smith (1974), Postmidnight chorus: A substorm
phenomenon, J. Geophys. Res., 79, 118-127.